NCERT Solution: Areas of Parallelograms and Triangles
In Fig.9.28, AP || BQ || CR. Prove that ar(AQC) = ar(PBR).
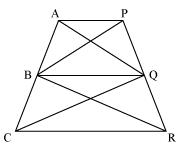
Answer
Given,
AP || BQ || CR
To Prove,
ar(AQC) = ar(PBR)
Proof:
ar(△AQB) = ar(△PBQ) --- (i) (On the same base BQ and between the same parallels AP and BQ.)
also,
ar(△BQC) = ar(△BQR) --- (ii) (On the same base BQ and between the same parallels BQ and CR.)
Adding (i) and (ii),
ar(△AQB) + ar(△BQC) = ar(△PBQ) + ar(△BQR)
⇒ ar(△ AQC) = ar(△ PBR)
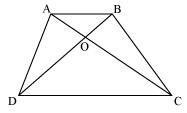
Answer
Given,
ar(△AOD) = ar(△BOC)
To Prove,
ABCD is a trapezium.
Proof:
ar(△AOD) = ar(△BOC)
⇒ ar(△AOD) + ar(△AOB) = ar(△BOC) + ar(△AOB)
⇒ ar(△ADB) = ar(△ACB)
Areas of △ADB and △ACB are equal. Therefore, they must lying between the same parallel lines.
Thus, AB ∥ CD
Therefore, ABCD is a trapezium.
Answer
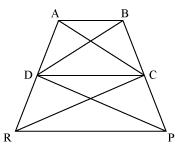
Given,
ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC)
To Prove,
ABCD and DCPR are trapeziums.
Proof:
ar(△BDP) = ar(△ARC)
⇒ ar(△BDP) - ar(△DPC) = ar(△DRC)
⇒ ar(△BDC) = ar(△ADC)
ar(△BDC) = ar(△ADC). Therefore, they must lying between the same parallel lines.
Thus, AB ∥ CD
Therefore, ABCD is a trapezium.
also,
ar(DRC) = ar(DPC). Therefore, they must lying between the same parallel lines.
Thus, DC ∥ PR
Therefore, DCPR is a trapezium.
Answer
As the parallelogram and the rectangle have the same base and equal area, therefore, these will also lie between the same parallels.
Consider the parallelogram ABCD and rectangle ABEF as follows.
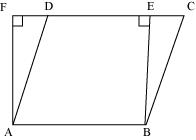
Here, it can be observed that parallelogram ABCD and rectangle ABEF are between the same parallels AB and CF.
We know that opposite sides of a parallelogram or a rectangle are of equal lengths. Therefore,
AB = EF (For rectangle)
AB = CD (For parallelogram)
∴ CD = EF
⇒ AB + CD = AB + EF ... (1)
Of all the line segments that can be drawn to a given line from a point not lying on it, the perpendicular line segment is the shortest.
∴ AF < AD
And similarly, BE < BC
∴ AF + BE < AD + BC ... (2)
From equations (1) and (2), we obtain
AB + EF + AF + BE < AD + BC + AB + CD
Perimeter of rectangle ABEF < Perimeter of parallelogram ABCD
In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

It is given that ABCD is a parallelogram. We know that opposite sides of a parallelogram are equal.
∴ AD = BC ... (1)
Similarly, for parallelograms DCEF and ABFE, it can be proved that
DE = CF ... (2)
And, EA = FB ... (3)
In ΔADE and ΔBCF,
AD = BC [Using equation (1)]
DE = CF [Using equation (2)]
EA = FB [Using equation (3)]
∴ ΔADE ≅ BCF (SSS congruence rule)
⇒ Area (ΔADE) = Area (ΔBCF)
In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that
ar (BPC) = ar (DPQ).
[Hint: Join AC.]

Answer :
It is given that ABCD is a parallelogram.
AD || BC and AB || DC(Opposite sides of a parallelogram are parallel to each other)
Join point A to point C.

Consider ΔAPC and ΔBPC
ΔAPC and ΔBPC are lying on the same base PC and between the same parallels PC and AB. Therefore,
Area (ΔAPC) = Area (ΔBPC) ... (1)
In quadrilateral ACDQ, it is given that
AD = CQ
Since ABCD is a parallelogram,
AD || BC (Opposite sides of a parallelogram are parallel)
CQ is a line segment which is obtained when line segment BC is produced.
∴ AD || CQ
We have,
AC = DQ and AC || DQ
Hence, ACQD is a parallelogram.
Consider ΔDCQ and ΔACQ
These are on the same base CQ and between the same parallels CQ and AD. Therefore,
Area (ΔDCQ) = Area (ΔACQ)
⇒ Area (ΔDCQ) - Area (ΔPQC) = Area (ΔACQ) - Area (ΔPQC)
⇒ Area (ΔDPQ) = Area (ΔAPC) ... (2)
From equations (1) and (2), we obtain
Area (ΔBPC) = Area (ΔDPQ)
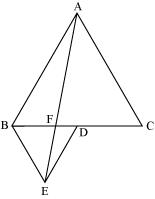
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) ar(BDE) = 1/4 ar(ABC)
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).
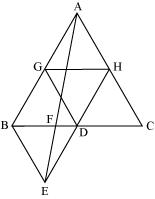
=> GH = 1/2 BC and GH || BD
=> GH = BD = DC and GH || BD (D is the mid-point of BC)
Consider quadrilateral GHDB.
GH ||BD and GH = BD
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area (ΔBDG) = Area (ΔHGD)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)
ar (ΔABC) = 4 x ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)