In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).

It is given that ABCD is a parallelogram. We know that opposite sides of a parallelogram are equal.

∴ AD = BC ... (1)

Similarly, for parallelograms DCEF and ABFE, it can be proved that

DE = CF ... (2)

And, EA = FB ... (3)

In ΔADE and ΔBCF,

AD = BC [Using equation (1)]

DE = CF [Using equation (2)]

EA = FB [Using equation (3)]

∴ ΔADE ≅ BCF (SSS congruence rule)

⇒ Area (ΔADE) = Area (ΔBCF)

In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that

ar (BPC) = ar (DPQ).

[Hint: Join AC.]

Answer :

 

It is given that ABCD is a parallelogram.

AD || BC and AB || DC(Opposite sides of a parallelogram are parallel to each other)

Join point A to point C.

Consider ΔAPC and ΔBPC

ΔAPC and ΔBPC are lying on the same base PC and between the same parallels PC and AB. Therefore,

Area (ΔAPC) = Area (ΔBPC) ... (1)

In quadrilateral ACDQ, it is given that

AD = CQ

Since ABCD is a parallelogram,

AD || BC (Opposite sides of a parallelogram are parallel)

CQ is a line segment which is obtained when line segment BC is produced.

∴ AD || CQ

We have,

AC = DQ and AC || DQ

Hence, ACQD is a parallelogram.

Consider ΔDCQ and ΔACQ

These are on the same base CQ and between the same parallels CQ and AD. Therefore,

Area (ΔDCQ) = Area (ΔACQ)

⇒ Area (ΔDCQ) - Area (ΔPQC) = Area (ΔACQ) - Area (ΔPQC)

⇒ Area (ΔDPQ) = Area (ΔAPC) ... (2)

From equations (1) and (2), we obtain

Area (ΔBPC) = Area (ΔDPQ)

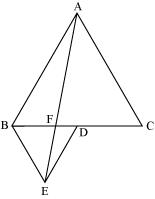
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

(i) ar(BDE) = 1/4 ar(ABC)

(i) Let G and H be the mid-points of side AB and AC respectively.

Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).

 

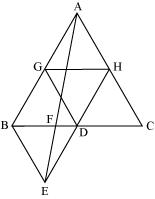
=> GH = 1/2 BC and GH || BD
=> GH = BD = DC and GH || BD (D is the mid-point of BC)


Consider quadrilateral GHDB.

GH ||BD and GH = BD

Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.

Therefore, BG = DH and BG || DH

Hence, quadrilateral GHDB is a parallelogram.

We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.

Hence, Area (ΔBDG) = Area (ΔHGD)

Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.

ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)

ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)

ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)

ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)

ar (ΔABC) = 4  x ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)

 

In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

(iii) ar(ABC) = 2 ar(BEC)

Area (ΔBDE) = Area (ΔAED) (Common base DE and DE||AB)

Area (ΔBDE) - Area (ΔFED) = Area (ΔAED) - Area (ΔFED)

Area (ΔBEF) = Area (ΔAFD) (1)

Area (ΔABD) = Area (ΔABF) + Area (ΔAFD)

Area (ΔABD) = Area (ΔABF) + Area (ΔBEF) [From equation (1)]

Area (ΔABD) = Area (ΔABE) (2)

AD is the median in ΔABC.

From (2) and (3), we obtain
2 ar (ΔBDE) = ar (ΔABE)

or ar(BDE) = 1/2 ar(BAE)

In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

(iii) ar(ABC) = 2 ar(BEC)

ANSWER

ar (ΔABE) = ar (ΔBEC) (Common base BE and BE||AC)

ar (ΔABF) + ar (ΔBEF) = ar (ΔBEC)

Using equation (1), we obtain

ar (ΔABF) + ar (ΔAFD) = ar (ΔBEC)

ar (ΔABD) = ar (ΔBEC)

1/2 ar(ΔABC) = ar(ΔBEC)
ar (ΔABC) = 2 ar (ΔBEC)

In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that

(iv) ar(BFE) =  ar(AFD)

ANSWER

(iv)It is seen that ΔBDE and ar ΔAED lie on the same base (DE) and between the parallels DE and AB.

∴ar (ΔBDE) = ar (ΔAED)

⇒ ar (ΔBDE) - ar (ΔFED) = ar (ΔAED) - ar (ΔFED)

∴ar (ΔBFE) = ar (ΔAFD)

In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (v) ar(BFE) = 2 ar(FED)

ANSWER:

Let h be the height of vertex E, corresponding to the side BD in ΔBDE.

Let H be the height of vertex A, corresponding to the side BC in ΔABC.

In (i), it was shown that ar(BDE) = 1/4 ar(ABC)

In (iv), it was shown that ar (ΔBFE) = ar (ΔAFD)

=>  ar (ΔBFE) = ar (ΔAFD)

= 2 ar (ΔFED)

Hence, ar(BFE) = 2 ar(FED)

In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (vi) ar(FED) = 1/8 ar(AFC)

ANSWER:

(vi) Area (AFC) = area (AFD) + area (ADC)