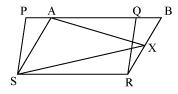
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS) 

Answer

 

(i) Parallelogram PQRS and ABRS lie on the same base SR and between the same parallel lines SR and PB.

∴ ar(PQRS) = ar(ABRS) --- (i)
(ii) In ΔAXS and parallelogram ABRS are lying on the same base AS and between the same parallel lines AS and BR.
∴ ar(ΔAXS) = 1/2 ar(ABRS) --- (ii)
From (i) and (ii),
ar(ΔAXS) = 1/2 ar(PQRS)

In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS) 

Answer

The field is divided into three parts. The three parts are in the shape of triangle. ΔPSA, ΔPAQ and ΔQAR.
Area of ΔPSA + ΔPAQ + ΔQAR = Area of PQRS --- (i) 
Area of ΔPAQ = 1/2 area of PQRS --- (ii)
Triangle and parallelogram on the same base and between the same parallel lines.
From (i) and (ii),
Area of ΔPSA + Area of ΔQAR = 1/2 area of PQRS --- (iii)
Clearly from (ii) and (iii),
Farmer must sow wheat or pulses in ΔPAQ or either in both ΔPSA and ΔQAR.

In Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar(ACE).

Answer

Given,

AD is median of ΔABC. Thus, it will divide ΔABC into two triangles of equal area.

∴ ar(ABD) = ar(ACD) --- (i)

also,

ED is the median of ΔABC.

∴ ar(EBD) = ar(ECD) --- (ii)

Subtracting (ii) from (i),

ar(ABD) - ar(EBD) = ar(ACD) - ar(ECD)

⇒ ar(ABE) = ar(ACE)

Answer

 

ar(BED) = (1/2) × BD × DE 
As E is the mid-point of AD,

Thus, AE = DE 
As AD is the median on side BC of triangle ABC, 
Thus, BD = DC 
Therefore,

DE = (1/2)AD --- (i)
BD = (1/2)BC --- (ii)

From (i) and (ii),

ar(BED) = (1/2) × (1/2) BC × (1/2)AD 
⇒ ar(BED) = (1/2) × (1/2) ar(ABC)

⇒ ar(BED) = 1/4 ar(ABC)

Answer

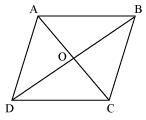
O is the mid point of AC and BD. (diagonals of bisect each other)

In ΔABC, BO is the median.

∴ ar(AOB) = ar(BOC) --- (i)

also,

In ΔBCD, CO is the median.

∴ ar(BOC) = ar(COD) --- (ii)

In ΔACD, OD is the median.

∴ ar(AOD) = ar(COD) --- (iii)

In ΔABD, AO is the median.

∴ ar(AOD) = ar(AOB) --- (iv)

From equations (i), (ii), (iii) and (iv),

ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)

So, the diagonals of a parallelogram divide it into four triangles of equal area.

In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that: ar(ABC) = ar(ABD).

Answer

In ΔABC,

AO is the median. (CD is bisected by AB at O)

∴ ar(AOC) = ar(AOD) --- (i) 

also, 

In ΔBCD,

BO is the median. (CD is bisected by AB at O)

∴ ar(BOC) = ar(BOD) --- (ii)
Adding (i) and (ii) we get,
ar(AOC) + ar(BOC) = ar(AOD) + ar(BOD)
⇒ ar(ABC) = ar(ABD)

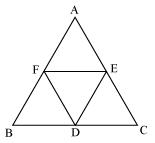
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC.
Show that
(i) BDEF is a parallelogram.         (ii) ar(DEF) = 1/4 ar(ABC)
(iii) ar (BDEF) = 1/2 ar(ABC)

Answer

Answer

In ΔABC,

AO is the median. (CD is bisected by AB at O)

∴ ar(AOC) = ar(AOD) --- (i) 

also, 

In ΔBCD,

BO is the median. (CD is bisected by AB at O)

∴ ar(BOC) = ar(BOD) --- (ii)
Adding (i) and (ii) we get,
ar(AOC) + ar(BOC) = ar(AOD) + ar(BOD)
⇒ ar(ABC) = ar(ABD)

In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:

(i) ar (DOC) = ar (AOB)

(ii) ar (DCB) = ar (ACB)

(iii) DA || CB or ABCD is a parallelogram.

[Hint: From D and B, draw perpendiculars to AC.]

Answer

Let us draw DN ⊥ AC and BM ⊥ AC.

(i) In ΔDON and ΔBOM,

∠ DNO = ∠ BMO (By construction)

∠ DON = ∠ BOM (Vertically opposite angles)

OD = OB (Given)

By AAS congruence rule,

ΔDON ≅ ΔBOM

∴ DN = BM ... (1)

We know that congruent triangles have equal areas.

∴ Area (ΔDON) = Area (ΔBOM) ... (2)

In ΔDNC and ΔBMA,

∠ DNC = ∠ BMA (By construction)

CD = AB (Given)

DN = BM [Using equation (1)]

∴ ΔDNC ≅ ΔBMA (RHS congruence rule)

⇒ Area (ΔDNC) = Area (ΔBMA) ... (3)

On adding equations (2) and (3), we obtain

Area (ΔDON) + Area (ΔDNC) = Area (ΔBOM) + Area (ΔBMA)

Therefore, Area (ΔDOC) = Area (ΔAOB)

(ii) We obtained,

Area (ΔDOC) = Area (ΔAOB)

⇒ Area (ΔDOC) + Area (ΔOCB) = Area (ΔAOB) + Area (ΔOCB)

(Adding Area (ΔOCB) to both sides)

⇒ Area (ΔDCB) = Area (ΔACB)

(iii) We obtained,

Area (ΔDCB) = Area (ΔACB)

If two triangles have the same base and equal areas, then these will lie between the same parallels.

∴ DA || CB ... (4)

In ΔDOA and ΔBOC,

∠ DOA = ∠ BOC (Vertically opposite angles)

OD = OB (Given)

∠ ODA = ∠ OBC (Alternate opposite angles)

By ASA congruence rule,

ΔDOA ≅ ΔBOC

∴ DA = BC ... (5)

In quadrilateral ABCD, one pair of opposite sides is equal and parallel (AD = BC)

Therefore, ABCD is a parallelogram.