
Electricity mcq
1. A cell, a resistor, a key and ammeter are arranged as shown in the circuit
diagrams of figure12.1. The current recorded in the ammeter will be
(a) maximum in (i)
(b) maximum in (ii)
(c) maximum in (iii)
(d) the same in all the cases
Ans. (d) The same in all the cases
Explanation: None of the conditions change in any of the circuits. Hence,
current would be same in all circuits.
2. In the following circuits (Figure 12.2), heat produced in the resistor or
combination of resistors connected to a 12 V battery will be
(a) same in all the cases
(b) minimum in case (i)
(c) maximum in case (ii)
(d) maximum in case (iii)
Ans. (c) Maximum in case (ii)
Explanation: In this case, two resistors are in series. Hence, their sum will be
equal to their arithmetic sum. In figure (iii) the total resistance will be less
than individual resistances because they are connected in parallel. A higher
resistance produces more heat so option (c) is correct.
3. Electrical resistivity of a given metallic wire depends upon
(a) its length
(b) its thickness
(c) its shape
(d) nature of the material
Ans. (d) Nature of the material
4. A current of 1 A is drawn by a filament of an electric bulb. Number of
electrons passing through a cross section of the filament in 16 seconds would be
roughly
(a) 1020
(b) 1016
(c) 1018
(d) 1023
ans A
Explanation: We have current I=1 A and time t=16s
We know;
I = Q / t or 1 A = Q/ 16 s
Q= 16C
Charge contained in 1 electron 1.6 x 10-19 C
So, 16 C charge is contained in following number of electrons;
![]()
5. Identify the circuit (Figure 12.3) in which the electrical components have
been properly connected.
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Ans. (b) (ii)
6. What is the maximum resistance which can be made using five resistors each of
1/5 Ω?
(a) 1/5 Ω
(b) 10 Ω
(c) 5 Ω
(d) 1 Ω
Ans. (d) 1Ω
7. What is the minimum resistance which can be made using five resistors each of
1/5 Ω ?
(a) 1/5 Ω
(b) 1/25 Ω
(c) 1/10 Ω
(d) 25 Ω
Ans. (b) 1/25 Ω
Explanation: When resistors are connected in parallel then we get the minimum
resistance out of the combination.
When given resistors are connected in parallel, the resistance of combination
can be calculated as follows:
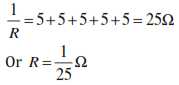
8. The proper representation of series combination of cells (Figure12.4)
obtaining maximum potential is
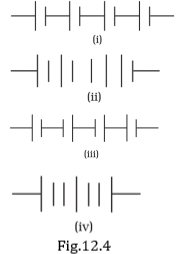
(a) (i)
(b) (ii)
(c) (iii)
(d) (iv)
Ans. (a) (i)
Explanation: In this combination, positive terminal of next cell is adjacent to
negative terminal of previous cell.