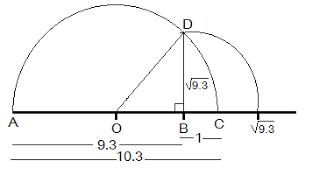
Represent √9.3 on the number line.
Step 1: Draw a line segment of unit 9.3. Extend it to C so that BC is of 1 unit.
Step 2: Now, AC = 10.3 units. Find the centre of AC and name it as O.
Step 3: Draw a semi circle with radius OC and centre O.
Step 4: Draw a perpendicular line BD to AC at point B which intersect the semicircle at D. Also, Join OD.
Step 5: Now, OBD is a right angled triangle.
Here, OD = 10.3/2 (radius of semi circle), OC = 10.3/2, BC = 1
OB = OC – BC = (10.3/2) – 1 = 8.3/2
Using Pythagoras theorem,
OD2 = BD2 + OB2
⇒ (10.3/2)2 = BD2 + (8.3/2)2
⇒ BD2 = (10.3/2)2 - (8.3/2)2
⇒ BD2 = (10.3/2 – 8.3/2) (10.3/2 + 8.3/2)
⇒ BD2 = 9.3
⇒ BD2 = √9.3
Thus, the length of BD is √9.3.
Step 6: Taking BD as radius and B as centre draw an arc which touches the line segment. The point where it touches the line segment is at a distance of √9.3 from O as shown in the figure.