
In Fig. 5.10, if AC = BD, then prove that AB = CD.
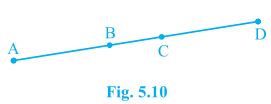
Given, AC = BD
From the figure,
AC = AB + BC
BD = BC + CD
⇒ AB + BC = BC + CD
According to Euclid's axiom, when equals are subtracted from equals, remainders are also equal.
Subtracting BC both sides,
AB + BC - BC = BC + CD - BC
AB = CD