
In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = 1/2(∠QOS – ∠POS).
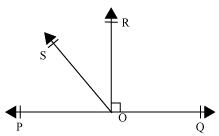
Given,
OR is perpendicular to line PQ
To prove,
∠ROS = 1/2(∠QOS – ∠POS)
A/q,
∠POR = ∠ROQ = 90° (Perpendicular)
∠QOS = ∠ROQ + ∠ROS = 90° + ∠ROS --- (i)
∠POS = ∠POR - ∠ROS = 90° - ∠ROS --- (ii)
Subtracting (ii) from (i)
∠QOS - ∠POS = 90° + ∠ROS - (90° - ∠ROS)
⇒ ∠QOS - ∠POS = 90° + ∠ROS - 90° + ∠ROS
⇒ ∠QOS - ∠POS = 2∠ROS
⇒ ∠ROS = 1/2(∠QOS – ∠POS)
Hence, Proved.