
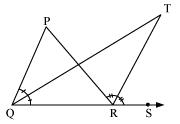
In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
AnswerGiven,
Bisectors of ∠PQR and ∠PRS meet at point T.
To prove,
∠QTR = 1/2∠QPR.
Proof,
∠TRS = ∠TQR +∠QTR (Exterior angle of a triangle equals to the sum of the two interior angles.)
⇒ ∠QTR = ∠TRS - ∠TQR --- (i)
also,
∠SRP = ∠QPR + ∠PQR
⇒ 2∠TRS = ∠QPR + 2∠TQR
⇒ ∠QPR = 2∠TRS - 2∠TQR
⇒ 1/2∠QPR = ∠TRS - ∠TQR --- (ii)
Equating (i) and (ii)
∠QTR - ∠TQR = 1/2∠QPR
Hence proved.