
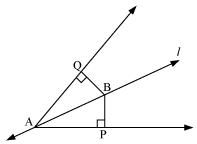
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig. 7.20). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Answer
Given,
l is the bisector of an angle ∠A.
BP and BQ are perpendiculars.
(i) In ΔAPB and ΔAQB,
∠P = ∠Q (Right angles)
∠BAP = ∠BAQ (l is bisector)
AB = AB (Common)
Therefore, ΔAPB ≅ ΔAQB by AAS congruence condition.
(ii) BP = BQ by CPCT. Therefore, B is equidistant from the arms of ∠A.