
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC
In ΔABC, AD is the perpendicular bisector of BC (see Fig. 7.30). Show that ΔABC is an isosceles triangle in which AB = AC.
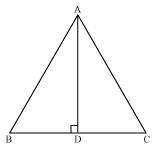
Answer
Given,
AD is the perpendicular bisector of BC
To show,
AB = AC
Proof,
In ΔADB and ΔADC,
AD = AD (Common)
∠ADB = ∠ADC
BD = CD (AD is the perpendicular bisector)
Therefore, ΔADB ≅ ΔADC by SAS congruence condition.
AB = AC (by CPCT)