
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see Fig. 7.31). Show that these altitudes are equal.
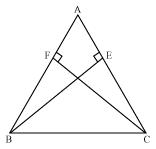
Answer
Given,
BE and CF are altitudes.
AC = AB
To show,
BE = CF
Proof,
In ΔAEB and ΔAFC,
∠A = ∠A (Common)
∠AEB = ∠AFC (Right angles)
AB = AC (Given)
Therefore, ΔAEB ≅ ΔAFC by AAS congruence condition.
Thus, BE = CF by CPCT.