
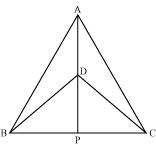
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that
(i) ΔABD ≅ ΔACD
(ii) ΔABP ≅ ΔACP
(iii) AP bisects ∠A as well as ∠D.
(iv) AP is the perpendicular bisector of BC.
Answer
Given,
ΔABC and ΔDBC are two isosceles triangles.
(i) In ΔABD and ΔACD,
AD = AD (Common)
AB = AC (ΔABC is isosceles)
BD = CD (ΔDBC is isosceles)
Therefore, ΔABD ≅ ΔACD by SSS congruence condition.
(ii) In ΔABP and ΔACP,
AP = AP (Common)
∠PAB = ∠PAC (ΔABD ≅ ΔACD so by CPCT)
AB = AC (ΔABC is isosceles)
Therefore, ΔABP ≅ ΔACP by SAS congruence condition.
(iii) ∠PAB = ∠PAC by CPCT as ΔABD ≅ ΔACD.
AP bisects ∠A. --- (i)
also,
In ΔBPD and ΔCPD,
PD = PD (Common)
BD = CD (ΔDBC is isosceles.)
BP = CP (ΔABP ≅ ΔACP so by CPCT.)
Therefore, ΔBPD ≅ ΔCPD by SSS congruence condition.
Thus, ∠BDP = ∠CDP by CPCT. --- (ii)
By (i) and (ii) we can say that AP bisects ∠A as well as ∠D.
(iv) ∠BPD = ∠CPD (by CPCT as ΔBPD ≅ ΔCPD)
and BP = CP --- (i)
also,
∠BPD + ∠CPD = 180° (BC is a straight line.)
⇒ 2∠BPD = 180°
⇒ ∠BPD = 90° ---(ii)
From (i) and (ii),
AP is the perpendicular bisector of BC.