
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
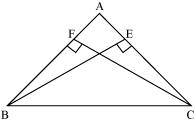
Given,
BE and CF are two equal altitudes.
In ΔBEC and ΔCFB,
∠BEC = ∠CFB = 90° (Altitudes)
BC = CB (Common)
BE = CF (Common)
Therefore, ΔBEC ≅ ΔCFB by RHS congruence condition.
Now,
∠C = ∠B (by CPCT)
Thus, AB = AC as sides opposite to the equal angles are equal.