
Show that the diagonals of a square are equal and bisect each other at right angles.
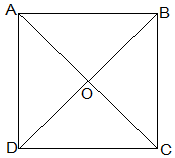
Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show,
AC = BD, AO = OC and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD,
BC = BA (Common)
∠ABC = ∠BAD = 90°
AC = AD (Given)
Therefore, ΔABC ≅ ΔBAD by SAS congruence condition.
Thus, AC = BD by CPCT. Therefore, diagonals are equal.
Now,
In ΔAOB and ΔCOD,
∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
Therefore, ΔAOB ≅ ΔCOD by AAS congruence condition.
Thus, AO = CO by CPCT. (Diagonal bisect each other.)
Now,
In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
Therefore, ΔAOB ≅ ΔCOB by SSS congruence condition.
also, ∠AOB = ∠COB
∠AOB + ∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90° (Diagonals bisect each other at right angles)