
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see Fig. 8.31). Show that the line segments AF and EC trisect the diagonal BD.
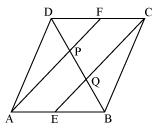
Given,
ABCD is a parallelogram. E and F are the mid-points of sides AB and CD respectively.
To show,
AF and EC trisect the diagonal BD.
Proof,
ABCD is a parallelogram
Therefor, AB || CD
also, AE || FC
Now,
AB = CD (Opposite sides of parallelogram ABCD)
⇒ 1/2 AB = 1/2 CD
⇒ AE = FC (E and F are midpoints of side AB and CD)
AECF is a parallelogram (AE and CF are parallel and equal to each other)
AF || EC (Opposite sides of a parallelogram)
Now,
In ΔDQC,
F is mid point of side DC and FP || CQ (as AF || EC).
P is the mid-point of DQ (Converse of mid-point theorem)
⇒ DP = PQ --- (i)
Similarly,
In APB,
E is mid point of side AB and EQ || AP (as AF || EC).
Q is the mid-point of PB (Converse of mid-point theorem)
⇒ PQ = QB --- (ii)
From equations (i) and (i),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.