
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
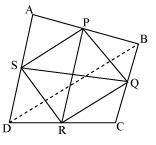
Let ABCD be a quadrilateral and P, Q, R and S are the mid points of AB, BC, CD and DA respectively.
Now,
In ΔACD,
R and S are the mid points of CD and DA respectively.
Thus, SR || AC.
Similarly we can show that,
PQ || AC
PS || BD
QR || BD
Thus, PQRS is parallelogram.
PR and QS are the diagonals of the parallelogram PQRS. So, they will bisect each other.