
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 1/2 AB
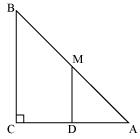
(i) In ΔACB,
M is the mid point of AB and MD || BC
Thus, D is the mid point of AC (Converse of mid point theorem)
(ii) ∠ACB = ∠ADM (Corresponding angles)
also, ∠ACB = 90°
Thus, ∠ADM = 90° and MD ⊥ AC
(iii) In ΔAMD and ΔCMD,
AD = CD (D is the midpoint of side AC)
∠ADM = ∠CDM (Each 90°)
DM = DM (common)
Thus, ΔAMD ≅ ΔCMD by SAS congruence condition.
AM = CM by CPCT
also, AM = 1/2 AB (M is mid point of AB)
Hence, CM = MA = 1/2 AB