
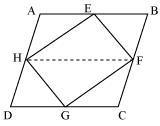
If E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 1/2 ar(ABCD).
If E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that
ar (EFGH) = 1/2 ar(ABCD).
Answer
Given,
E,F,G and H are respectively the mid-points of the sides of a parallelogram ABCD.
To Prove,
ar (EFGH) = 1/2 ar(ABCD)
Construction,
H and F are joined.
Proof,
AD || BC and AD = BC (Opposite sides of a parallelogram)
⇒ 1/2 AD = 1/2 BC
Also,
AH || BF and and DH || CF
⇒ AH = BF and DH = CF (H and F are mid points)
Thus, ABFH and HFCD are parallelograms.
Now,
ΔEFH and ||gm ABFH lie on the same base FH and between the same parallel lines AB and HF.
∴ area of EFH = 1/2 area of ABFH --- (i)
also, area of GHF = 1/2 area of HFCD --- (ii)
Adding (i) and (ii),
area of ΔEFH + area of ΔGHF = 1/2 area of ABFH + 1/2 area of HFCD
⇒ area of EFGH = area of ABFH
⇒ ar (EFGH) = 1/2 ar(ABCD)