
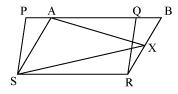
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = 1/2 ar (PQRS)
Answer
(i) Parallelogram PQRS and ABRS lie on the same base SR and between the same parallel lines SR and PB.
∴ ar(PQRS) = ar(ABRS) --- (i)
(ii) In ΔAXS and parallelogram ABRS are lying on the same base AS and between the same parallel lines AS and BR.
∴ ar(ΔAXS) = 1/2 ar(ABRS) --- (ii)
From (i) and (ii),
ar(ΔAXS) = 1/2 ar(PQRS)