
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer
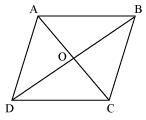
O is the mid point of AC and BD. (diagonals of bisect each other)
In ΔABC, BO is the median.
∴ ar(AOB) = ar(BOC) --- (i)
also,
In ΔBCD, CO is the median.
∴ ar(BOC) = ar(COD) --- (ii)
In ΔACD, OD is the median.
∴ ar(AOD) = ar(COD) --- (iii)
In ΔABD, AO is the median.
∴ ar(AOD) = ar(AOB) --- (iv)
From equations (i), (ii), (iii) and (iv),
ar(BOC) = ar(COD) = ar(AOD) = ar(AOB)
So, the diagonals of a parallelogram divide it into four triangles of equal area.