
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC.
Show that
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC.
Show that
(i) BDEF is a parallelogram. (ii) ar(DEF) = 1/4 ar(ABC)
(iii) ar (BDEF) = 1/2 ar(ABC)
Answer
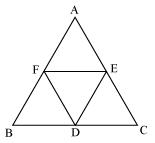
Answer
In ΔABC,
AO is the median. (CD is bisected by AB at O)
∴ ar(AOC) = ar(AOD) --- (i)
also,
In ΔBCD,
BO is the median. (CD is bisected by AB at O)
∴ ar(BOC) = ar(BOD) --- (ii)
Adding (i) and (ii) we get,
ar(AOC) + ar(BOC) = ar(AOD) + ar(BOD)
⇒ ar(ABC) = ar(ABD)