
XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and E respectively, show that ar (ABE) = ar (ACF)
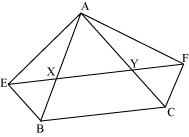
Answer
Given,
XY || BC, BE || AC and CF || AB
To show,
ar(ΔABE) = ar(ΔAC)
Proof:
EY || BC (XY || BC) --- (i)
also,
BE∥ CY (BE || AC) --- (ii)
From (i) and (ii),
BEYC is a parallelogram. (Both the pairs of opposite sides are parallel.)
Similarly,
BXFC is a parallelogram.
Parallelograms on the same base BC and between the same parallels EF and BC.
⇒ ar(BEYC) = ar(BXFC) (Parallelograms on the same base BC and between the same parallels EF and BC) --- (iii)
Also,
△AEB and parallelogram BEYC are on the same base BE and between the same parallels BE and AC.
⇒ ar(△AEB) = 1/2ar(BEYC) --- (iv)
Similarly,
△ACF and parallelogram BXFC on the same base CF and between the same parallels CF and AB.
⇒ ar(△ ACF) = 1/2ar(BXFC) --- (v)
From (iii), (iv) and (v),
ar(△AEB) = ar(△ACF)