
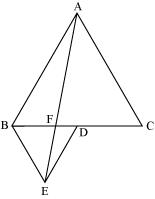
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) ar(BDE) = 1/4 ar(ABC)
(i) Let G and H be the mid-points of side AB and AC respectively.
Line segment GH is joining the mid-points. Therefore, it will be parallel to third side BC and also its length will be half of the length of BC (mid-point theorem).
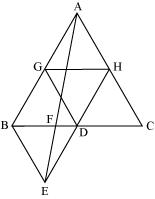
=> GH = 1/2 BC and GH || BD
=> GH = BD = DC and GH || BD (D is the mid-point of BC)
Consider quadrilateral GHDB.
GH ||BD and GH = BD
Two line segments joining two parallel line segments of equal length will also be equal and parallel to each other.
Therefore, BG = DH and BG || DH
Hence, quadrilateral GHDB is a parallelogram.
We know that in a parallelogram, the diagonal bisects it into two triangles of equal area.
Hence, Area (ΔBDG) = Area (ΔHGD)
Similarly, it can be proved that quadrilaterals DCHG, GDHA, and BEDG are parallelograms and their respective diagonals are dividing them into two triangles of equal area.
ar (ΔGDH) = ar (ΔCHD) (For parallelogram DCHG)
ar (ΔGDH) = ar (ΔHAG) (For parallelogram GDHA)
ar (ΔBDE) = ar (ΔDBG) (For parallelogram BEDG)
ar (ΔABC) = ar(ΔBDG) + ar(ΔGDH) + ar(ΔDCH) + ar(ΔAGH)
ar (ΔABC) = 4 x ar(ΔBDE)
Hence, ar(BDE) = 1/4 ar(ABC)