
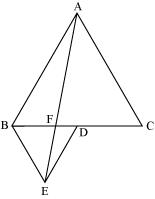
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (iv) ar(BFE) = ar(AFD)
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(iv) ar(BFE) = ar(AFD)
ANSWER
(iv)It is seen that ΔBDE and ar ΔAED lie on the same base (DE) and between the parallels DE and AB.
∴ar (ΔBDE) = ar (ΔAED)
⇒ ar (ΔBDE) - ar (ΔFED) = ar (ΔAED) - ar (ΔFED)
∴ar (ΔBFE) = ar (ΔAFD)