
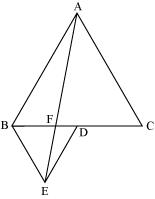
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (v) ar(BFE) = 2 ar(FED)
In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that (v) ar(BFE) = 2 ar(FED)
ANSWER:
Let h be the height of vertex E, corresponding to the side BD in ΔBDE.
Let H be the height of vertex A, corresponding to the side BC in ΔABC.
In (i), it was shown that ar(BDE) = 1/4 ar(ABC)
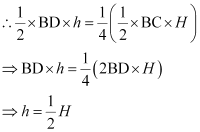
In (iv), it was shown that ar (ΔBFE) = ar (ΔAFD)
=> ar (ΔBFE) = ar (ΔAFD)
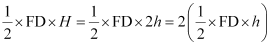
= 2 ar (ΔFED)
Hence, ar(BFE) = 2 ar(FED)