
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Given,
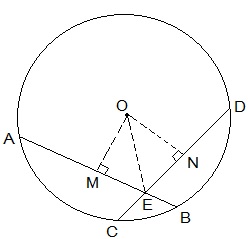
AB and CD are chords intersecting at E.
AB = CD
To prove,
AE = DE and CE = BE
Construction,
OM ⊥ AB and ON ⊥ CD. OE is joined.
Proof,
OM bisects AB (OM ⊥ AB)
ON bisects CD (ON ⊥ CD)
As AB = CD thus,
AM = ND --- (i)
and MB = CN --- (ii)
In ΔOME and ΔONE,
∠OME = ∠ONE (Perpendiculars)
OE = OE (Common)
OM = ON (AB = CD and thus equidistant from the centre)
ΔOME ≅ ΔONE by RHS congruence condition.
ME = EN by CPCT --- (iii)
From (i) and (ii) we get,
AM + ME = ND + EN
⇒ AE = ED
From (ii) and (iii) we get,
MB - ME = CN - EN
⇒ EB = CE