
A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.
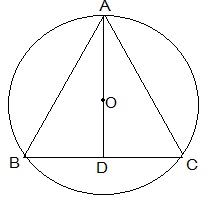
Let A, B and C represent the positions of Ankur, Syed and David respectively. All three boys at equal distances thus ABC is an equilateral triangle.
AD ⊥ BC is drawn. Now, AD is median of ΔABC and it passes through the centre O.
Also, O is the centroid of the ΔABC. OA is the radius of the triangle.
OA = 2/3 AD
Let the side of a triangle a metres then BD = a/2 m.
Applying Pythagoras theorem in ΔABD,
AB2 = BD2 + AD2
⇒ AD2 = AB2 - BD2
⇒ AD2 = a2 - (a/2)2
⇒ AD2 = 3a2/4
⇒ AD = √3a/2
OA = 2/3 AD ⇒ 20 m = 2/3 × √3a/2
⇒ a = 20√3 m
Length of the string is 20√3 m.