
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram.
Solution
Given,
Area of the parallelogram and triangle are equal.
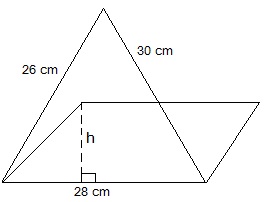
Length of the sides of the triangle are 26 cm, 28 cm and 30 cm.
Perimeter of the triangle = 26 + 28 + 30 = 84 cm
Semi perimeter of the triangle = 84/2 cm = 42 cm
Using heron's formula,
Area of the triangle = √s (s-a) (s-b) (s-c)
= √42(42 - 26) (46 - 28) (46 - 30) cm2
= √46 × 16 × 14 × 16 cm2
= 336 cm2Let height of parallelogram be h.
Area of parallelogram = Area of triangle
28cm × h = 336 cm2
⇒ h = 336/28 cm
⇒ h = 12 cm
The height of the parallelogram is 12 cm.