
A rhombus shaped field has green grass for 18 cows to graze. If each side of the rhombus is 30 m and its longer diagonal is 48 m, how much area of grass field will each cow be getting?
Solution
Diagonal AC divides the rhombus ABCD into two congruent triangles of equal area.
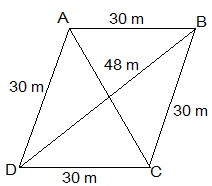
Semi perimeter of ΔABC = (30 + 30 + 48)/2 m = 54 m
Using heron's formula,
Area of the ΔABC = √s (s-a) (s-b) (s-c)
= √54(54 - 30) (54 - 30) (54 - 48) m2
= √54 × 24 × 24 × 6 cm2
= 432 m2
Area of field = 2 × area of the ΔABC = (2 × 432)m2 = 864 m2
Thus,
Area of grass field which each cow will be getting = 864/18 m2 = 48 m2