
A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field.
Solution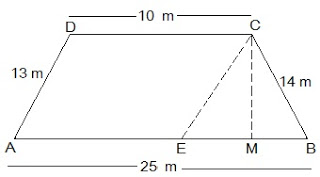
Let ABCD be the given trapezium with parallel sides AB = 25m and CD = 10mand the non-parallel sides AD = 13m and BC = 14m.
CM ⊥ AB and CE || AD.
In ΔBCE,
BC = 14m, CE = AD = 13 m and
BE = AB - AE = 25 - 10 = 15m
Semi perimeter of the ΔBCE = (15 + 13 + 14)/2 m = 21 m
Using heron's formula,
Area of the ΔBCE = √s (s-a) (s-b) (s-c)
= √21(21 - 14) (21 - 13) (21 - 15) m2
= √21 × 7 × 8 × 6 m2
= 84 m2
also, area of the ΔBCE = 1/2 × BE × CM = 84 m2
⇒ 1/2 × 15 × CM = 84 m2
⇒ CM = 168/15 m2
⇒ CM = 56/5 m2
Area of the parallelogram AECD = Base × Altitude = AE × CM = 10 × 84/5 = 112 m2
Area of the trapezium ABCD = Area of AECD + Area of ΔBCE
= (112+ 84) m2 = 196 m2