
You have studied in Class IX that a median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
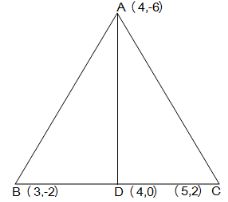
Let the vertices of the triangle be A (4, -6), B (3, -2), and C (5, 2).
Let D be the mid-point of side BC of ΔABC. Therefore, AD is the median in ΔABC.
Coordinates of point D = (3+5/2, -2+2/2) = (4,0)
Area of a triangle = 1/2 {x1 (y2 - y3) + x2 (y3 - y1) + x3 (y1 - y2)}
Area of ΔABD = 1/2 [(4) {(-2) - (0)} + 3{(0) - (-6)} + (4) {(-6) - (-2)}]
= 1/2 (-8+18-16)
= -3 square units
However, area cannot be negative. Therefore, area of ΔABD is 3 square units.
Area of ΔABD = 1/2 [(4) {0 - (2)} + 4{(2) - (-6)} + (5) {(-6) - (0)}]
= 1/2 (-8+32-30)
= -3 square units
However, area cannot be negative. Therefore, area of ΔABD is 3 square units.
The area of both sides is same. Thus, median AD has divided ΔABC in two triangles of equal areas.