
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
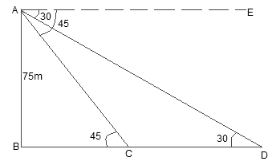
Let AB be the lighthouse of height 75 m.
Let C and D be the positions of the ships.
30° and 45° are the angles of depression from the lighthouse.
In right ΔABC,
tan 45° = AB/BC
⇒ 1= 75/BC
⇒ BC = 75 m
also,
In right ΔABD,
tan 30° = AB/BD
⇒ 1/√3 = 75/BD
⇒ BD = 75√3 m
The distance between the two ships = CD = BD - BC = (75√3 - 75) m = 75(√3-1) m.