
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) √119 cm
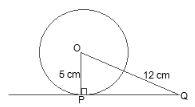
The line drawn from the centre of the circle to the tangent is perpendicular to the tangent.
∴ OP ⊥ PQ
By Pythagoras theorem in ΔOPQ,
OQ2 = OP2 + PQ2
⇒ (12)2 = 52 + PQ2
⇒PQ2 = 144 - 25
⇒PQ2 = 119
⇒PQ = √119 cm
(D) is the correct option.