
A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
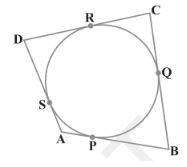
From the figure we observe that,
DR = DS (Tangents on the circle from point D) … (i)
AP = AS (Tangents on the circle from point A) … (ii)
BP = BQ (Tangents on the circle from point B) … (iii)
CR = CQ (Tangents on the circle from point C) … (iv)
Adding all these equations,
DR + AP + BP + CR = DS + AS + BQ + CQ
⇒ (BP + AP) + (DR + CR) = (DS + AS) + (CQ + BQ)
⇒ CD + AB = AD + BC