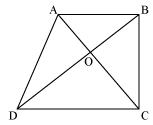
It can be observed that ΔDAC and ΔDBC lie on the same base DC and between the same parallels AB and CD.

∴ Area (ΔDAC) = Area (ΔDBC)

⇒ Area (ΔDAC) - Area (ΔDOC) = Area (ΔDBC) - Area (ΔDOC)

⇒ Area (ΔAOD) = Area (ΔBOC)

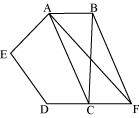
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

(i) ar (ACB) = ar (ACF)

(ii) ar (AEDF) = ar (ABCDE)

Answer :

(i) ΔACB and ΔACF lie on the same base AC and are between

The same parallels AC and BF.

∴ Area (ΔACB) = Area (ΔACF)

(ii) It can be observed that

Area (ΔACB) = Area (ΔACF)

⇒ Area (ΔACB) + Area (ACDE) = Area (ACF) + Area (ACDE)

⇒ Area (ABCDE) = Area (AEDF)

Answer

Let ABCD be the plot of the land of the shape of a quadrilateral.

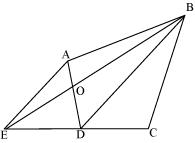
Construction,

Diagonal BD is joined. AE is drawn parallel BD. BE is joined which intersected AD at O. △BCE is the shape of the original field and △AOB is the area for constructing health centre. Also, △DEO land joined to the plot.
To prove:
ar(△DEO) = ar(△AOB)
Proof:
△DEB and △DAB lie on the same base BD and between the same parallel lines BD and AE.
ar(△DEB) = ar(△DAB)
⇒ ar(△DEB) - ar△DOB) = ar(△DAB) - ar(△DOB) 

⇒ ar(△DEO) = ar(△AOB)

Answer

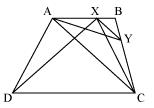
Given,

ABCD is a trapezium with AB || DC.

XY || AC

Construction,

CX is joined.

To Prove,

ar(ADX) = ar(ACY)

Proof:

ar(△ADX) = ar(△AXC) --- (i) (On the same base AX and between the same parallels AB and CD)
also,

ar(△ AXC)=ar(△ ACY) --- (ii) (On the same base AC and between the same parallels XY and AC.)

From (i) and (ii),

ar(△ADX)=ar(△ACY)

In Fig.9.28, AP || BQ || CR. Prove that ar(AQC) = ar(PBR).

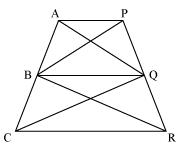
Answer

 

Given,

AP || BQ || CR

To Prove,

ar(AQC) = ar(PBR)

Proof:

ar(△AQB) = ar(△PBQ) --- (i) (On the same base BQ and between the same parallels AP and BQ.)

also,

ar(△BQC) = ar(△BQR) --- (ii) (On the same base BQ and between the same parallels BQ and CR.)

Adding (i) and (ii),
ar(△AQB) + ar(△BQC) = ar(△PBQ) + ar(△BQR) 

⇒ ar(△ AQC) = ar(△ PBR)

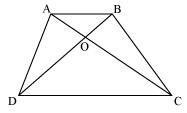
Answer

Given,
ar(△AOD) = ar(△BOC)

To Prove,

ABCD is a trapezium.

Proof:

ar(△AOD) = ar(△BOC)

⇒ ar(△AOD) + ar(△AOB) = ar(△BOC) + ar(△AOB) 

⇒ ar(△ADB) = ar(△ACB)

Areas of △ADB and △ACB are equal. Therefore, they must lying between the same parallel lines.
Thus, AB ∥  CD

Therefore, ABCD is a trapezium.

Answer

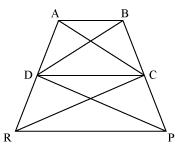
Given,

ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC)

To Prove,

ABCD and DCPR are trapeziums.

Proof:

ar(△BDP) = ar(△ARC)

⇒ ar(△BDP) - ar(△DPC) = ar(△DRC)

⇒ ar(△BDC) = ar(△ADC)

ar(△BDC) = ar(△ADC). Therefore, they must lying between the same parallel lines.

Thus, AB ∥ CD

Therefore, ABCD is a trapezium.

also,

ar(DRC) = ar(DPC). Therefore, they must lying between the same parallel lines.

Thus, DC ∥ PR

Therefore, DCPR is a trapezium.

Answer

As the parallelogram and the rectangle have the same base and equal area, therefore, these will also lie between the same parallels.

Consider the parallelogram ABCD and rectangle ABEF as follows.

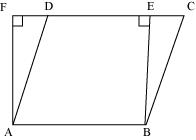
Here, it can be observed that parallelogram ABCD and rectangle ABEF are between the same parallels AB and CF.

We know that opposite sides of a parallelogram or a rectangle are of equal lengths. Therefore,

AB = EF (For rectangle)

AB = CD (For parallelogram)

∴ CD = EF

⇒ AB + CD = AB + EF ... (1)

Of all the line segments that can be drawn to a given line from a point not lying on it, the perpendicular line segment is the shortest.

∴ AF < AD

And similarly, BE < BC

∴ AF + BE < AD + BC ... (2)

From equations (1) and (2), we obtain

AB + EF + AF + BE < AD + BC + AB + CD

Perimeter of rectangle ABEF < Perimeter of parallelogram ABCD