A circle can have infinite tangents.

(i) one

(ii) secant

(iii) two

(iv) point of contact

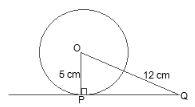
The line drawn from the centre of the circle to the tangent is perpendicular to the tangent.
∴ OP ⊥ PQ

By Pythagoras theorem in ΔOPQ,

OQ² = OP² + PQ²
⇒ (12)² = 5² + PQ²

⇒PQ² = 144 - 25

⇒PQ² = 119

⇒PQ = √119 cm

(D) is the correct option.

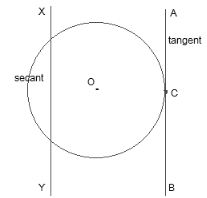
AB and XY are two parallel lines where AB is the tangent to the circle at point C while XY is the secant to the circle.

The line drawn from the centre of the circle to the tangent is perpendicular to the tangent.

∴ OP ⊥ PQ
also, ΔOPQ is right angled.
OQ = 25 cm and PQ = 24 cm (Given)

By Pythagoras theorem in ΔOPQ,

OQ² = OP² + PQ²
⇒ (25)² = OP² + (24)²

⇒ OP² = 625 - 576

⇒ OP² = 49

⇒ OP = 7 cm

The radius of the circle is option (A) 7 cm.

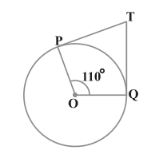
OP and OQ are radii of the circle to the tangents TP and TQ respectively.
∴ OP ⊥ TP and,
∴ OQ ⊥ TQ
∠OPT = ∠OQT = 90°
In quadrilateral POQT,
Sum of all interior angles = 360°
∠PTQ + ∠OPT + ∠POQ + ∠OQT  = 360°
⇒ ∠PTQ + 90° + 110° + 90°  = 360°

⇒ ∠PTQ = 70°

∠PTQ is equal to option (B) 70°.

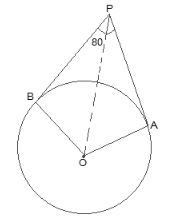
OA and OB are radii of the circle to the tangents PA and PB respectively.
∴ OA ⊥ PA and,
∴ OB ⊥ PB
∠OBP = ∠OAP = 90°

In quadrilateral AOBP,
Sum of all interior angles = 360°
∠AOB + ∠OBP + ∠OAP + ∠APB  = 360°
⇒ ∠AOB + 90° + 90° + 80°  = 360°

⇒ ∠AOB = 100°

Now,

In ΔOPB and ΔOPA,
AP = BP (Tangents from a point are equal)
OA = OB (Radii of the circle)
OP = OP (Common side)
∴ ΔOPB ≅ ΔOPA (by SSS congruence condition)

Thus ∠POB = ∠POA

∠AOB = ∠POB + ∠POA

⇒ 2 ∠POA = ∠AOB

⇒ ∠POA = 100°/2 = 50°

∠POA is equal to option  (A) 50°

Let AB be a diameter of the circle. Two tangents PQ and RS are drawn at points A and B respectively.

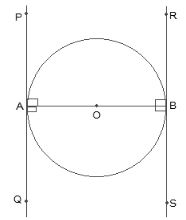
Radii of the circle to the tangents will be perpendicular to it.
∴ OB ⊥ RS and,

∴ OA ⊥ PQ
∠OBR = ∠OBS = ∠OAP = ∠OAQ = 90º

From the figure,
∠OBR = ∠OAQ (Alternate interior angles)
∠OBS = ∠OAP (Alternate interior angles)
Since alternate interior angles are equal, lines PQ and RS will be parallel.

Hence Proved that the tangents drawn at the ends of a diameter of a circle are parallel.