According to the equation of motion under gravity:
v² − u² = 2 gs
Where,
u = Initial velocity of the stone = 0
v = Final velocity of the stone
s = Height of the stone = 19.6 m
g = Acceleration due to gravity = 9.8 m s⁻²
∴ v² − 0² = 2 � 9.8 � 19.6
v2 = 2 � 9.8 � 19.6 = (19.6)²
v = 19.6 m s^{− 1}
Hence, the velocity of the stone just before touching the ground is 19.6 m s⁻¹.

According to the equation of motion under gravity:
v² − u² = 2 gs
Where,
u = Initial velocity of the stone = 40 m/s
v = Final velocity of the stone = 0
s = Height of the stone 
g = Acceleration due to gravity = −10 m s⁻²
Let h be the maximum height attained by the stone. 
Therefore, 
0 - (40)² = 2 x h x (-10)
h= 40 x 40 / 20 = 80 m

Therefore, total distance covered by the stone during its upward and downward journey = 80 + 80 = 160 m
Net displacement of the stone during its upward and downward journey
= 80 + (−80) = 0

According to question,

M_Sun = Mass of the Sun = 2 � 10³⁰ kg
M_Earth = Mass of the Earth = 6 � 10²⁴ kg
R = Average distance between the Earth and the Sun = 1.5 � 1011 m
From Universal law of gravitation,

Let the two stones meet after a time t.

(i) For the stone dropped from the tower:

Initial velocity, u= 0

Let the displacement of the stone in time t from the top of the tower be s.

Acceleration due to gravity, g = 9.8 m s^{- 2}

From the equation of motion,

(ii) For the stone thrown upwards:

Initial velocity, u= 25 m s^{- 1}

Let the displacement of the stone from the ground in time tbe s'.

Acceleration due to gravity, g = - 9.8 m s ^{- 2}

Equation of motion,



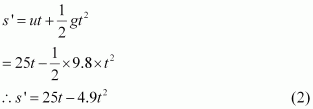
The combined displacement of both the stones at the meeting point is equal to the height of the tower 100 m.



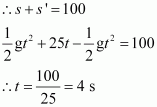
In 4 s, the falling stone has covered a distance given by equation (1) as



Therefore, the stones will meet after 4 s

A ball thrown up vertically returns to the thrower after 6 s. Find
(a) the velocity with which it was thrown up,
(b) the maximum height it reaches, and
(c) its position after 4 s.

Answer

(a) Time of ascent is equal to the time of descent. The ball takes a total of 6 s for its upward and downward journey.
Hence, it has taken 3 s to attain the maximum height.
Final velocity of the ball at the maximum height, v = 0 
Acceleration due to gravity, g = −9.8 m s⁻²
Equation of motion, v = u + gt will give,
0 = u + (−9.8 × 3)
u = 9.8 × 3 = 29.4 ms⁻¹
Hence, the ball was thrown upwards with a velocity of 29.4 m s⁻¹.

(b) Let the maximum height attained by the ball be h.
Initial velocity during the upward journey, u = 29.4 m s⁻¹
Final velocity, v = 0
Acceleration due to gravity, g = −9.8 m s⁻²
From the equation of motion, s= ut + 1/2 at²
h= 29.4 x 3 + 1/2 x -9.8 x (3)² = 44.1 m

(c) Ball attains the maximum height after 3 s. After attaining this height, it will start falling downwards. 
In this case,
Initial velocity, u = 0
Position of the ball after 4 s of the throw is given by the distance travelled by it during its downward journey in 4 s − 3 s = 1 s.
Equation of motion, s= ut + 1/2 gt² will give,
s= 0 x t + 1/2 x 9.8 x 1² = 4.9 m
Total height = 44.1 m
This means that the ball is 39.2 m (44.1 m − 4.9 m) above the ground after 4 seconds.

An object immersed in a liquid experiences buoyant force in the upward direction.

For an object immersed in water two force acts on it
→ gravitational force which tends to pull object in downward direction
→ buoyant force that pushes the object in upward direction
here in this case buoyant force is greater than the gravitational pull on the plastic block. This is the reason the plastic block comes up to the surface of the water as soon as it is released under water.

If the density of an object is more than the density of a liquid, then it sinks in the liquid. On the other hand, if the density of an object is less than the density of a liquid, then it floats on the surface of the liquid.
Here, density of the substance = Mass of the substance / Volume of the substance
= 50 / 20
= 2.5 g cm^-3
The density of the substance is more than the density of water (1 g cm⁻³). Hence, the substance will sink in water.