The power P of a lens of focal length f is given by the relationP= 1/f

(i) Power of the lens used for correcting distant vision = – 5.5 D
Focal length of the required lens, f= 1/Pf= 1/-5.5 = -0.181 m
The focal length of the lens for correcting distant vision is – 0.181 m.

(ii) Power of the lens used for correcting near vision = +1.5 D
Focal length of the required lens, f= 1/P

f= 1/1.5 = +0.667 m
The focal length of the lens for correcting near vision is 0.667 m.

The person is suffering from an eye defect called myopia. In this defect, the image is formed in front of the retina. Hence, a concave lens is used to correct this defect of vision.

Object distance, u = infinity = ∞
Image distance, v = � 80 cm
Focal length = f
According to the lens formula,



We know,

P= 1 / f (metres)

P = 1/ -0.8  = -1.25


A concave lens of power - 1.25 D is required by the person to correct his defect.

A person suffering from hypermetropia can see distinct objects clearly but faces difficulty in seeing nearby objects clearly. It happens because the eye lens focuses the incoming divergent rays beyond the retina. This defect of vision is corrected by using a convex lens. A convex lens of suitable power converges the incoming light in such a way that the image is formed on the retina, as shown in the following figure.



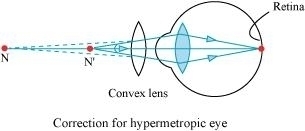
The convex lens actually creates a virtual image of a nearby object (N' in the figure) at the near point of vision (N) of the person suffering from hypermetropia.

The given person will be able to clearly see the object kept at 25 cm (near point of the normal eye), if the image of the object is formed at his near point, which is given as 1 m.

Object distance, u = - 25 cm

Image distance, v = - 1 m = - 100 m

Focal length, f

Using the lens formula,

P= 1 / f (metres)

P = 1/ 0.33 m  = + 3.0 D

A convex lens of power +3.0 D is required to correct the defect.

A normal eye is unable to clearly see the objects placed closer than 25 cm because the ciliary muscles of eyes are unable to contract beyond a certain limit.

The image is formed on the retina even on increasing the distance of an object from the eye. For this
eye lens becomes thinner and its focal length increases as the object is moved away from the eye.

Stars twinkle due to atmospheric refraction of starlight. As the stars are very far away, they behave as almost point sources of light. A son account of atmospheric refraction, the path of rays of light coming from the star goes on varying slightly, the apparent position of the star fluctuates and the amount of starlight entering the eye flickers. So, sometimes, the star appears brighter and at some other time, fainter. Thus, the stars twinkle.

Planets do not twinkle because they appear larger in size than the stars as they are relatively closer to earth. Planets can be considered as a collection of a large number of point-size sources of light. The different parts of these planets produce either brighter or dimmer effect in such a way that the average of brighter and dimmer effect is zero. Hence, the twinkling effects of the planets are nullified and they do not twinkle.

During sunrise, the light rays coming from the Sun have to travel a greater distance in the earth’s atmosphere before reaching our eyes. In this journey, the shorter wavelengths of lights are scattered out and only longer wavelengths are able to reach our eyes. Since blue colour has a shorter wavelength and red colour has a longer wavelength, the red colour is able to reach our eyes after the atmospheric scattering of light. Therefore, the Sun appears reddish early in the morning.