In Δ ABC,∠B = 90º
By Applying Pythagoras theorem , we get

AC² = AB² + BC² = (24)² + 7² = (576+49) cm² = 625 cm²
⇒ AC = 25

(i) sin A = BC/AC = 7/25   
cos A = AB/AC = 24/25

(ii) sin C = AB/AC = 24/25
     cos C = BC/AC = 7/25

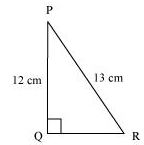
By Applying Pythagoras theorem in ΔPQR , we get
PR² = PQ² + QR² = (13)² = (12)² + QR² = 169 = 144  + QR²
⇒  QR² = 25 ⇒  QR = 5 cm

Now,
tan P = QR/PQ = 5/12
cot R = QR/PQ = 5/12
A/q
tan P – cot R = 5/12 - 5/12 = 0

Let ΔABC be a right-angled triangle, right-angled at B.

We know that sin A = BC/AC = 3/4

Let BC be 3k and AC will be 4k where k is a positive real number.
 

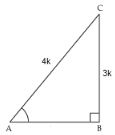
By Pythagoras theorem we get,
AC² = AB² + BC² 
(4k)² = AB² + (3k)²
16k² - 9k² = AB²
AB² = 7k²
AB = √7 k

cos A = AB/AC = √7 k/4k = √7/4

tan A = BC/AB = 3k/√7 k = 3/√7

Let ΔABC be a right-angled triangle, right-angled at B.

We know that cot A = AB/BC = 8/15   (Given)
Let AB be 8k and BC will be 15k where k is a positive real number. 

By Pythagoras theorem we get,
AC² = AB² + BC² 
AC² = (8k)² + (15k)²
AC² = 64k² + 225k²
AC² = 289k²
AC = 17 k

sin A = BC/AC = 15k/17k = 15/17

sec A = AC/AB = 17k/8 k = 17/8

 

Let ΔABC be a right-angled triangle, right-angled at B.

We know that sec θ = OP/OM = 13/12   (Given)
Let OP be 13k and OM will be 12k where k is a positive real number. 
By Pythagoras theorem we get,
OP² = OM² + MP² 
(13k)² = (12k)² + MP² 
169k² - 144k² = MP²
MP² = 25k²

MP = 5

Now,

sin θ = MP/OP = 5k/13k = 5/13

cos θ = OM/OP = 12k/13k = 12/13

tan θ = MP/OM = 5k/12k = 5/12

cot θ = OM/MP = 12k/5k = 12/5

cosec θ = OP/MP = 13k/5k = 13/5

Let ΔABC in which CD ⊥ AB.

A/q,

cos A = cos B

⇒ AD/AC = BD/BC

⇒ AD/BD = AC/BC

Let AD/BD = AC/BC = k

⇒ AD = kBD  .... (i)

⇒ AC = kBC  .... (ii)

By applying Pythagoras theorem in ΔCAD and ΔCBD we get,
CD² = AC² - AD² …. (iii)
and also CD² = BC² - BD² …. (iv)
From equations (iii) and (iv) we get,
AC² - AD² = BC² - BD²
⇒ (kBC)² - (k BD)² = BC² - BD²
⇒ k² (BC² - BD²) = BC² - BD²
⇒ k² = 1
⇒ k = 1
Putting this value in equation (ii), we obtain
AC = BC
⇒ ∠A = ∠B  (Angles opposite to equal sides of a triangle are equal-isosceles triangle)

Let ΔABC in which ∠B = 90º and ∠C = θ

cot θ = BC/AB = 7/8

Let BC = 7k and AB = 8k, where k is a positive real number.
By Pythagoras theorem in ΔABC we get.
AC² = AB² + BC² 
AC² = (8k)² + (7k)²
AC² = 64k² + 49k²
AC² = 113k²
AC = √113 k

Let ΔABC in which ∠B = 90º,

cot A = AB/BC = 4/3
Let AB = 4k and BC = 3k, where k is a positive real number.
By Pythagoras theorem in ΔABC we get.
AC² = AB² + BC² 
AC² = (4k)² + (3k)²
AC² = 16k² + 9k²
AC² = 25k²
AC = 5k
tan A = BC/AB = 3/4
sin A = BC/AC = 3/5
cos A = AB/AC = 4/5