(i)

If BC is k, then AB will be√3, where k is a positive integer.

In ΔABC,

AC² = AB² + BC²

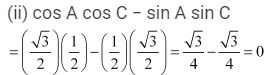
⇒ tan (A + B) = tan 60°

⇒ tan (A - B) = tan 30°
⇒ (A - B) = 30° ... (ii)

(i) False.
Let A = 30° and B = 60°, then
sin (A + B) = sin (30° + 60°) = sin 90° = 1 and,
sin A + sin B = sin 30° + sin 60°

= 1/2 + √3/2 = 1+√3/2

(ii) True.

sin 0° = 0

sin 30° = 1/2

sin 45° = 1/√2

sin 60° = √3/2

sin  90° = 1

Thus the value of sin θ increases as θ increases.

(iii) False.

cos 0° = 1

cos 30° = √3/2

cos 45° = 1/√2

cos 60° = 1/2

cos 90° = 0

Thus the value of cos θ decreases as θ increases.

(iv) sin θ = cos θ for all values of θ.

This is true when θ = 45° 

It is not true for all other values of θ.

Hence, the given statement is false.

(v) True.

cot A = cos A/sin A

cot 0° = cos 0°/sin 0° = 1/0 = undefined.

(i) sin 18°/cos 72°

    = sin (90° - 18°) /cos 72° 

    = cos 72° /cos 72° = 1

(ii) tan 26°/cot 64°

    = tan (90° - 36°)/cot 64°

    = cot 64°/cot 64° = 1

(iii) cos 48° - sin 42°

      = cos (90° - 42°) - sin 42°

      = sin 42° - sin 42° = 0

(iv) cosec 31° - sec 59°

     = cosec (90° - 59°) - sec 59°
     = sec 59° - sec 59° = 0

(i) tan 48° tan 23° tan 42° tan 67°
    = tan (90° - 42°) tan (90° - 67°) tan 42° tan 67°
    = cot 42° cot 67° tan 42° tan 67°
    = (cot 42° tan 42°) (cot 67° tan 67°) = 1×1 = 1

(ii) cos 38° cos 52° - sin 38° sin 52°
    = cos (90° - 52°) cos (90°-38°) - sin 38° sin 52°
    = sin 52° sin 38° - sin 38° sin 52° = 0

Given that,

tan 2A = cot (A− 18°)

cot (90° − 2A) = cot (A −18°)

90° − 2A = A− 18°

108° = 3A

A = 36°