Given,
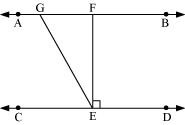
AB || CD
EF ⊥ CD
∠GED = 126°
A/q,
∠FED = 90° (EF ⊥ CD)
Now,
∠AGE = ∠GED (Since, AB || CD and GE is transversal. Alternate interior angles.)
∴ ∠AGE = 126°
Also, ∠GEF = ∠GED - ∠FED
⇒ ∠GEF = 126° - 90°
⇒ ∠GEF = 36°
Now,
∠FGE +∠AGE = 180° (Linear pair)
⇒ ∠FGE = 180° - 126°
⇒ ∠FGE = 54°

Given,

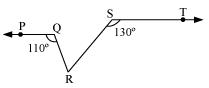
PQ || ST, ∠PQR = 110° and ∠RST = 130°

Construction,

A line XY parallel to PQ and ST is drawn.

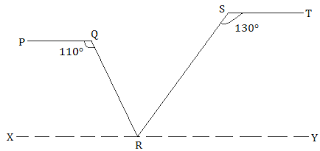
∠PQR + ∠QRX = 180° (Angles on the same side of transversal.)
⇒ 110° + ∠QRX = 180°
⇒ ∠QRX = 70°
Also,
∠RST + ∠SRY = 180° (Angles on the same side of transversal.) 
⇒ 130° + ∠SRY = 180°
⇒ ∠SRY = 50°
Now,
∠QRX +∠SRY + ∠QRS = 180°
⇒ 70° + 50° + ∠QRS = 180°
⇒ ∠QRS = 60°

Given,
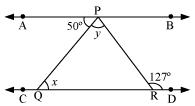
AB || CD, ∠APQ = 50° and ∠PRD = 127°
A/q,
x = 50° (Alternate interior angles.)
∠PRD + ∠RPB = 180° (Angles on the same side of transversal.)
⇒ 127° + ∠RPB = 180°
⇒ ∠RPB = 53° 
Now,
y + 50° + ∠RPB = 180° (AB is a straight line.)
⇒ y + 50° + 53° = 180°
⇒ y + 103° = 180°
⇒ y = 77°

In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

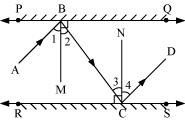
ANSWER:

Let us draw BE ⟂ PQ and CF ⟂ RS.

 As PQ || RS
So, BE || CF

By laws of reflection we know that,

Angle of incidence = Angle of reflection

Thus, ∠1 = ∠2 and ∠3 = ∠4  --- (i)

also, ∠2 = ∠3     (alternate interior angles because BE || CF and a transversal line BC cuts them at B and C)    --- (ii)

From (i) and (ii),

∠1 + ∠2 = ∠3 + ∠4

⇒ ∠ABC = ∠DCB

⇒ AB || CD      (alternate interior angles are equal)

1. In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.

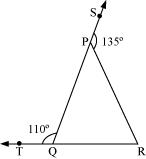
Answer

Given,
∠SPR = 135° and ∠PQT = 110°
A/q,
∠SPR +∠QPR = 180° (SQ is a straight line.)
⇒ 135° +∠QPR = 180°
⇒ ∠QPR = 45°
also,
∠PQT +∠PQR = 180° (TR is a straight line.)
⇒ 110° +∠PQR = 180°
⇒ ∠PQR = 70°
Now,
∠PQR +∠QPR + ∠PRQ = 180° (Sum of the interior angles of the triangle.)
⇒ 70° + 45° + ∠PRQ = 180°
⇒ 115° + ∠PRQ = 180° 
⇒ ∠PRQ = 65°

In Fig. 6.40, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of Δ XYZ, find ∠OZY and ∠YOZ.

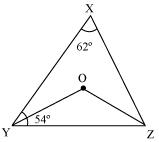
Answer
Given,
∠X = 62°, ∠XYZ = 54°
YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively.
A/q,
∠X +∠XYZ + ∠XZY = 180° (Sum of the interior angles of the triangle.)
⇒ 62° + 54° + ∠XZY = 180°
⇒ 116° + ∠XZY = 180°
⇒ ∠XZY = 64°
Now,
∠OZY = 1/2∠XZY (ZO is the bisector.)
⇒ ∠OZY = 32°
also,
∠OYZ = 1/2∠XYZ (YO is the bisector.)
⇒ ∠OYZ = 27°
Now,
∠OZY +∠OYZ + ∠O = 180° (Sum of the interior angles of the triangle.)
⇒ 32° + 27° + ∠O = 180°
⇒ 59° + ∠O = 180°
⇒ ∠O = 121°

In Fig. 6.41, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.

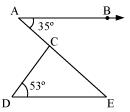
Answer

Given,
AB || DE, ∠BAC = 35° and ∠ CDE = 53°
A/q,
∠BAC = ∠CED (Alternate interior angles.)
∴ ∠CED = 35°
Now,
∠DCE +∠CED + ∠CDE = 180° (Sum of the interior angles of the triangle.)
⇒ ∠DCE + 35° + 53° = 180°
⇒ ∠DCE + 88° = 180°
⇒ ∠DCE = 92°

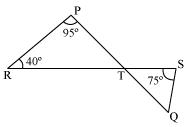
In Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.

Answer

Given,
∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75° 
A/q,
∠PRT +∠RPT + ∠PTR = 180° (Sum of the interior angles of the triangle.)
⇒ 40° + 95° + ∠PTR = 180°
⇒ 40° + 95° + ∠PTR = 180° 
⇒ 135° + ∠PTR = 180°
⇒ ∠PTR = 45°
∠PTR = ∠STQ = 45° (Vertically opposite angles.)
Now,
∠TSQ +∠PTR + ∠SQT = 180° (Sum of the interior angles of the triangle.)
⇒ 75° + 45° + ∠SQT = 180°
⇒ 120° + ∠SQT = 180° 
⇒ ∠SQT = 60°