Initial speed of the train, u= 90 km/h = 25 m/s
Final speed of the train, v = 0 (finally the train comes to rest)
Acceleration = - 0.5 m s^-2
According to third equation of motion:
v²= u²+ 2 as
(0)2= (25)²+ 2 ( -0.5) s

Where, s is the distance covered by the train



The train will cover a distance of 625 m before it comes to rest.

Initial Velocity of trolley, u= 0 cms^-1
Acceleration, a= 2 cm s-2
Time, t= 3 s
We know that final velocity, v= u + at = 0 + 2 x 3 cms^-1
Therefore, The velocity of train after 3 seconds = 6 cms^-1

Initial Velocity of the car, u=0 ms^-1
Acceleration, a= 4 m s^-2
Time, t= 10 s
We know Distance, s= ut + (1/2)at²
Therefore, Distance covered by car in 10 second= 0 × 10 + (1/2) × 4 × 10²
= 0 + (1/2) × 4× 10 × 10 m
= (1/2)× 400 m
= 200 m

Initially, velocity of the stone,u= 5 m/s

Final velocity, v= 0 (since the stone comes to rest when it reaches its maximum height)

Acceleration of the stone, a= acceleration due to gravity, g = 10 m/s²

(in downward direction)

There will be a change in the sign of acceleration because the stone is being thrown upwards.

Acceleration, a = - 10 m/s²

Let s be the maximum height attained by the stone in time t.

According to the first equation of motion:

v= u + at

0 = 5 + ( - 10)t
t= -5 / -10 = 0.5 s

According to the third equation of motion:

v² = u²+ 2as

(0)²= (5)²+ 2( - 10) s

s= 5² / 20 =1.25 m

Hence, the stone attains a height of 1.25 m in 0.5 s.

Diameter of circular track (D) = 200 m
Radius of circular track (r) = 200 / 2=100 m
Time taken by the athlete for one round (t) = 40 s
Distance covered by athlete in one round (s) = 2π r
= 2 � ( 22 / 7 ) � 100
Speed of the athlete (v) = Distance / Time
= (2 � 2200) / (7 � 40)
= 4400 / 7 � 40
Therefore, Distance covered in 140 s = Speed (s) � Time(t)
= 4400 / (7 � 40) � (2 � 60 + 20)
= 4400 / (7 � 40) � 140
= 4400 � 140 /7 � 40
= 2200 m

Number of round in 40 s =1 round
Number of round in 140 s =140/40
=3 1/2
After taking start from position X,the athlete will be at postion Y after 3 1/2 rounds as shown in figure

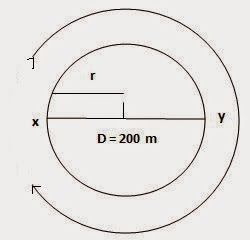
Hence, Displacement of the athlete with respect to initial position at x= xy
= Diameter of circular track
= 200 m

Total Distance covered from AB = 300 m
Total time taken = 2 × 60 + 30 s
=150 s

Therefore, Average Speed from AB = Total Distance / Total Time
=300 / 150 m s^-1
=2 m s^-1
Therefore, Velocity from AB =Displacement AB / Time = 300 / 150 m s^-1
=2 m s^-1
Total Distance covered from AC =AB + BC
=300 + 200 m

Total time taken from A to C = Time taken for AB + Time taken for BC
= (2 × 60+30)+60 s
= 210 s
Therefore, Average Speed from AC = Total Distance /Total Time
= 400 /210 m s^-1
= 1.904 m s^-1

Displacement (S) from A to C = AB - BC
= 300-100 m
= 200 m

Time (t) taken for displacement from AC = 210 s

Therefore, Velocity from AC = Displacement (s) / Time(t)
= 200 / 210 m s^-1
= 0.952 m s^-1

The distance Abdul commutes while driving from Home to School = S
Let us assume time taken by Abdul to commutes this distance = t₁
Distance Abdul commutes while driving from School to Home = S
Let us assume time taken by Abdul to commutes this distance = t₂
Average speed from home to school v_1av = 20 km h^-1
Average speed from school to home v_2av = 30 km h^-1
Also we know Time taken form Home to School t₁ =S / v_1av
Similarly Time taken form School to Home t₂ =S/v_2av
Total distance from home to school and backward = 2 S
Total time taken from home to school and backward (T) = S/20+ S/30
Therefore, Average speed (Vav) for covering total distance (2S) = Total Distance/Total Time
= 2S / (S/20 +S/30)
= 2S / [(30S+20S)/600]
= 1200S / 50S
= 24 kmh^-1

Given Initial velocity of motorboat,  u = 0
Acceleration of motorboat,  a = 3.0 m s^-2
Time under consideration,  t = 8.0 s
We know that Distance, s = ut + (1/2)at²
Therefore, The distance travel by motorboat = 0 ×8 + (1/2)3.0 × 8²
= (1/2) × 3 × 8 × 8 m
= 96 m