Find the zero of the polynomial in each of the following cases:
(i) p(x) = x + 5 

(ii) p(x) = x - 5 

(iii) p(x) = 2x + 5
(iv) p(x) = 3x - 2 

(v) p(x) = 3x 

(vi) p(x) = ax, a ≠ 0
(vii) p(x) = cx + d, c ≠ 0, c, are real numbers.

 

Answer

 

(i) p(x) = x + 5 

p(x) = 0

x + 5 = 0

x = -5

Therefore, x = -5 is a zero of polynomial p(x) = x + 5 .

 

(ii) p(x) = x - 5

p(x) = 0

x - 5 = 0

x = 5

Therefore, x = 5 is a zero of polynomial p(x) = x - 5.

 

(iii) p(x) = 2x + 5

p(x) = 0

2x + 5 = 0
2x = -5
x = -5/2
Therefore, x = -5/2 is a zero of polynomial p(x) = 2x + 5.

(iv) p(x) = 3x - 2
p(x) = 0
3x - 2 = 0
x = 2/3
Therefore, x = 2/3 is a zero of polynomial p(x) = 3x - 2.

(v) p(x) = 3x
p(x) = 0
3x = 0
x = 0
Therefore, x = 0 is a zero of polynomial p(x) = 3x.

(vi) p(x) = ax
p(x) = 0
ax = 0
x = 0
Therefore, x = 0 is a zero of polynomial p(x) = ax.

(vii) p(x) = cx + d
p(x) = 0
cx + d = 0
x = -d/c
Therefore, x = -d/c is a zero of polynomial p(x) = cx + d.

By Long Division,

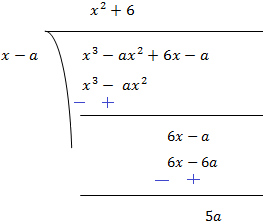
Therefore, remainder obtained is 5a when x³ - ax² + 6x - a is divided by x - a

We have to divide 3x³ + 7x by 7 + 3x. If remainder comes out to be 0 then 7 + 3x will be a factor of 3x³ + 7x.
By Long Division,

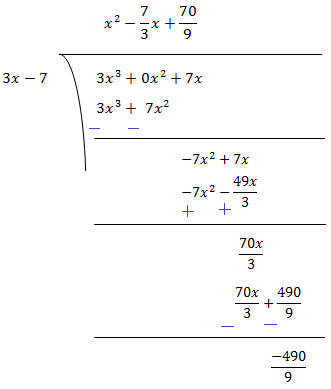
As remainder is not zero so 7 + 3x is not a factor of 3x³ + 7x.

Determine which of the following polynomials has (x + 1) a factor:
(i) x³ + x² + x + 1

(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1 

(iv) x³ - x² - (2 + √2)x + √2

Answer

(i) If (x + 1) is a factor of p(x) = x³ + x² + x + 1, p(-1) must be zero. 
Here, p(x) = x³ + x² + x + 1 
p(-1) = (-1)³ + (-1)² + (-1) + 1 
= -1 + 1 - 1 + 1 = 0
Therefore, x + 1 is a factor of this polynomial

(ii) If (x + 1) is a factor of p(x) = x⁴ + x³ + x² + x + 1, p(-1) must be zero. 
Here, p(x) = x⁴ + x³ + x² + x + 1 
p(-1) = (-1)⁴ + (-1)³ + (-1)² + (-1) + 1
= 1 - 1 + 1 - 1 + 1 = 1

As, p(-1) ≠ 0
Therefore, x + 1 is not a factor of this polynomial

(iii)If (x + 1) is a factor of polynomial p(x) = x⁴ + 3x³ + 3x² + x + 1, p(- 1) must be 0. 
p(-1) = (-1)⁴ + 3(-1)³ + 3(-1)² + (-1) + 1
= 1 - 3 + 3 - 1 + 1 = 1
As, p(-1) ≠ 0
Therefore, x + 1 is not a factor of this polynomial.

 

(iv) If (x + 1) is a factor of polynomial

p(x) = x³ - x² - (2 + √2)x + √2, p(- 1) must be 0.

p(-1) =  (-1)³ -  (-1)² -  (2 + √2) (-1) + √2
= -1 - 1 + 2 + √2 + √2
=2√2
As, p(-1) ≠ 0
Therefore,, x + 1 is not a factor of this polynomial.

Use the Factor Theorem to determine whether g(x) is a factor of p(x) in each of the following cases:
(i) p(x) = 2x³ + x² - 2x - 1, g(x) = x + 1
(ii) p(x) = x³ + 3x² + 3x + 1, g(x) = x + 2
(iii) p(x) = x³ - 4 x² + x + 6, g(x) = x - 3

Answer

(i) If g(x) = x + 1 is a factor of given polynomial p(x), p(- 1) must be zero.
p(x) = 2x³ + x² - 2x - 1
p(- 1) = 2(-1)³ + (-1)² - 2(-1) - 1
= 2(- 1) + 1 + 2 - 1 = 0
Hence, g(x) = x + 1 is a factor of given polynomial.

(ii) If g(x) = x + 2 is a factor of given polynomial p(x), p(- 2) must be 0.
p(x) = x³ +3x² + 3x + 1
p(-2) = (-2)³ + 3(- 2)² + 3(- 2) + 1
= -8 + 12 - 6 + 1
= -1

As, p(-2) ≠ 0

Hence g(x) = x + 2 is not a factor of given polynomial.

(iii) If g(x) = x - 3 is a factor of given polynomial p(x), p(3) must be 0.
p(x) = x³ - 4x² + x + 6
p(3) = (3)³ - 4(3)² + 3 + 6
= 27 - 36 + 9 = 0
Therefore,, g(x) = x - 3 is a factor of given polynomial.

Find the value of k, if x - 1 is a factor of p(x) in each of the following cases:(i) p(x) = x² + x + k
(ii) p(x) = 2x² + kx +  √2
(iii) p(x) = kx² - √2x + 1
(iv) p(x) = kx² - 3x + k

Answer

(i) If x - 1 is a factor of polynomial p(x) = x² + x + k, then

p(1) = 0
⇒ (1)² + 1 + k = 0
⇒ 2 + k = 0
⇒ k = - 2

Therefore, value of k is -2.

(ii) If x - 1 is a factor of polynomial p(x) = 2x² + kx +  √2, then
p(1) = 0
⇒ 2(1)² + k(1) + √2 = 0
⇒ 2 + k + √2 = 0
⇒ k = -2 - √2 = -(2 + √2)

Therefore, value of k is -(2 + √2).

(iii) If x - 1 is a factor of polynomial p(x) = kx² - √2x + 1, then
p(1) = 0
⇒ k(1)² - √2(1) + 1 = 0
⇒ k - √2 + 1 = 0
⇒ k = √2 - 1

Therefore, value of k is √2 - 1.

(iv) If x - 1 is a factor of polynomial p(x) = kx² - 3x + k, then
p(1) = 0
⇒ k(1)² + 3(1) + k = 0
⇒ k - 3 + k = 0
⇒ 2k - 3 = 0
⇒ k = 3/2

Therefore, value of k is 3/2.

Factorise:
(i) 12x² + 7x + 1
(ii) 2x² + 7x + 3
(iii) 6x² + 5x - 6
(iv) 3x² - x - 4 

Answer

(i) 12x² + 7x + 1
= 12x² - 4x - 3x+ 1                   
= 4x (3x - 1) - 1 (3x - 1)
= (3x - 1) (4x - 1)

(ii) 2x² + 7x + 3
= 2x² + 6x + x + 3
= 2x (x + 3) + 1 (x + 3)
=  (x + 3) (2x + 1) 

(iii) 6x² + 5x - 6
= 6x² + 9x - 4x - 6

 = 3x (2x + 3) - 2 (2x + 3)
= (2x + 3) (3x - 2)

(iv) 3x² - x - 4
= 3x² - 4x + 3x - 4 
= x (3x - 4) + 1 (3x - 4)
= (3x - 4) (x + 1)