CBSE - Polynomials

1 Polynomials 

If a and b are the zeros of the quadratic polynomial p(s) = 3s² – 6s + 4, find the value of 
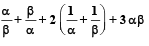 is

1) 4
2) 8
3) 6
4) 3

2 Polynomials 

p(x) = x⁴ -6x³ +16x² -25x +10
     q(x) = x²-2x+k
It is given
p(x) = r(x) q(x) + (x+a)
Find the value of k and a

1) 2,-2
2) 5 ,-5
3) 7,3
4) 3,-1
 

3 Polynomials 

Find the remainder  when x⁴+x³-2x²+x+1 is divided by x-1

1) 1
2) 5 
3) 2 
4) 3 

4 Polynomials 

If α  and  β are zeroes of the polynomial f(x)=x²+px+q then find the quadratic polynomial  having 1/α and 1/β as its zeroes

1) 2
2) 1
3) -1
4) 0

5 Polynomials 

The zeroes of the quadratic polynomial x² + 99x + 127 are

1) both positive
2) both negative
3) both equal
4) one positive and one negative

6 Polynomials 

If one of the zeroes of the cubic polynomial ax³ + bx² + cx + d is zero, the product of then other two zeroes is

1) -c/a 
2) c/a 
3) 0 
4) -b/a 

7 Polynomials 

If the zeroes of the quadratic polynomial ax² + bx + c, c ≠ 0 are equal, then
1) c and a have opposite signs
2) c and b have opposite signs
3) c and a have the same sign
4) c and b have the same sign

8 Polynomials 

If the polynomial  x³ + 2x² - αx - 12   is divided by   (x - 4)  the remainder is 52. Find the value of 

1) 11 / 2
2) - 5
3) 8
4)  - 8

9 Polynomials 

If α, β are the zeros of the polynomial f(x) = x² + x + 1, then =

1) 1
2) -1
3) 0
4) None of these

10 Polynomials 

If one of the zeroes of the quadratic polynomial (k-1)x² + kx + 1 is -3,then the value of k is 
1) -4/3
2) 4/3
3) 2/3
4) -2/3